Isochrones, mésochrones : comment cartographier des données temporelles

Qu’est-ce qu’une isochrone ?

Dans le domaine des transports, on définit une isochrone à partir d’une position O (l’origine) et d’un temps t. On appelle alors isochrone l’ensemble des positions qui sont accessibles depuis O en un temps inférieur à t.^{1 2}

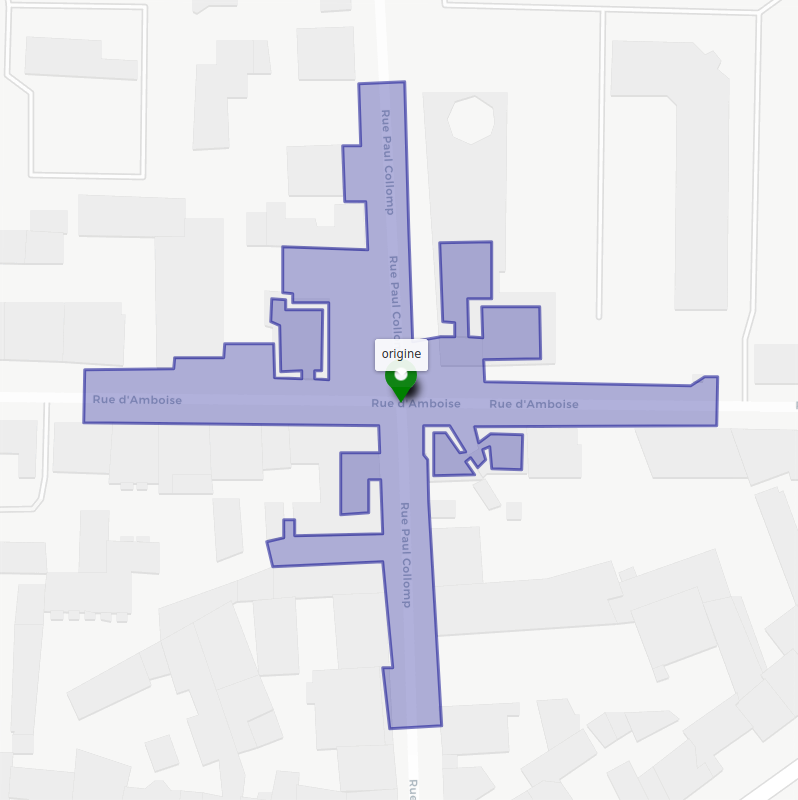
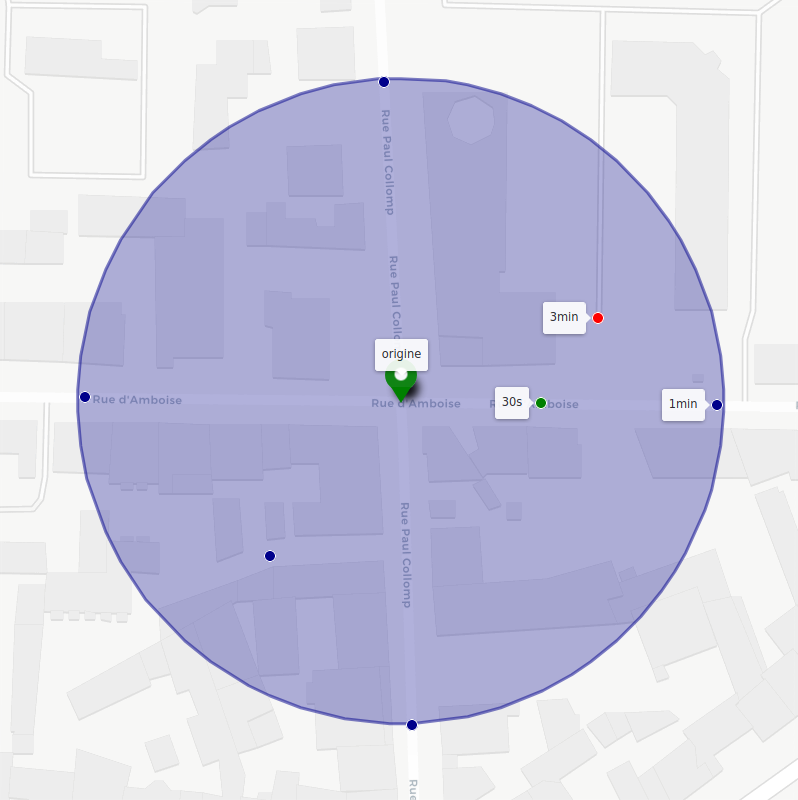
Cette figure représente l’isochrone à 1 min depuis l’origine indiquée sur la carte. Bien que cette zone représente effectivement l’ensemble des points qu’il est possible d’atteindre en moins d’une minute, son calcul exact est en général impossible pour de nombreuses raisons, notamment et en premier lieu à cause de la précision et de la quantité des données de terrain qui seraient nécessaires. Aussi, on procède en général à une approximation en recherchant les points du réseau connu accessibles dans le temps donné. On construit ensuite un polygone basé sur ces points qui sert d’approximation à notre isochrone.

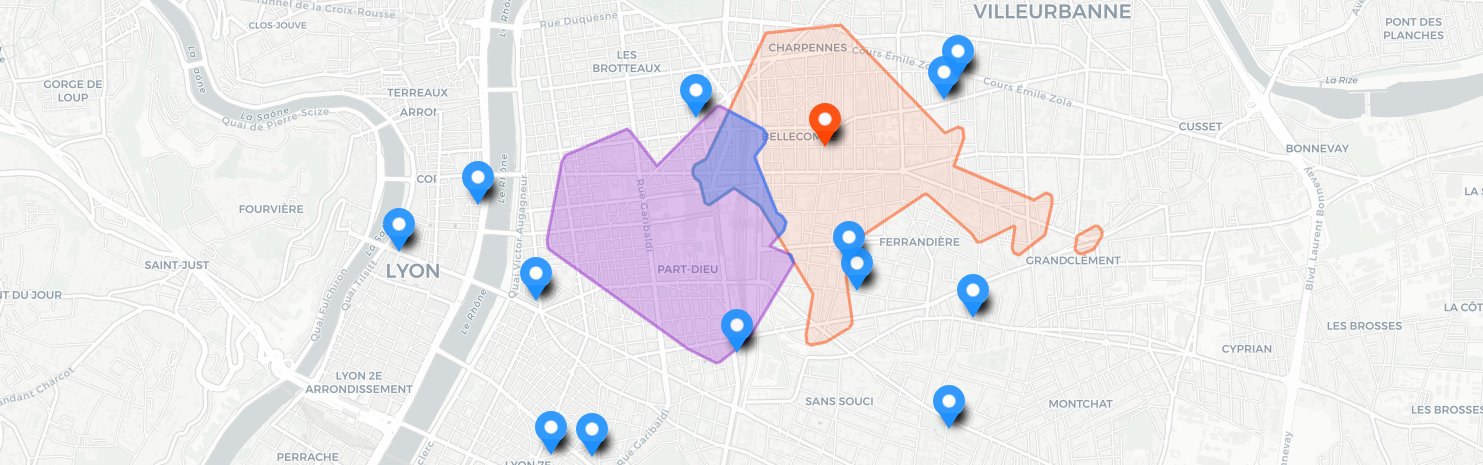
Sur la figure suivante sont représentés quelques points remarquables : les points bleus sont accessibles en 1 minute depuis l’origine, le vert en 30 secondes et le rouge en 3 minutes. On a construit un polygone dont les sommets sont tous les points accessibles en 1 minute comme approximation à notre isochrone.

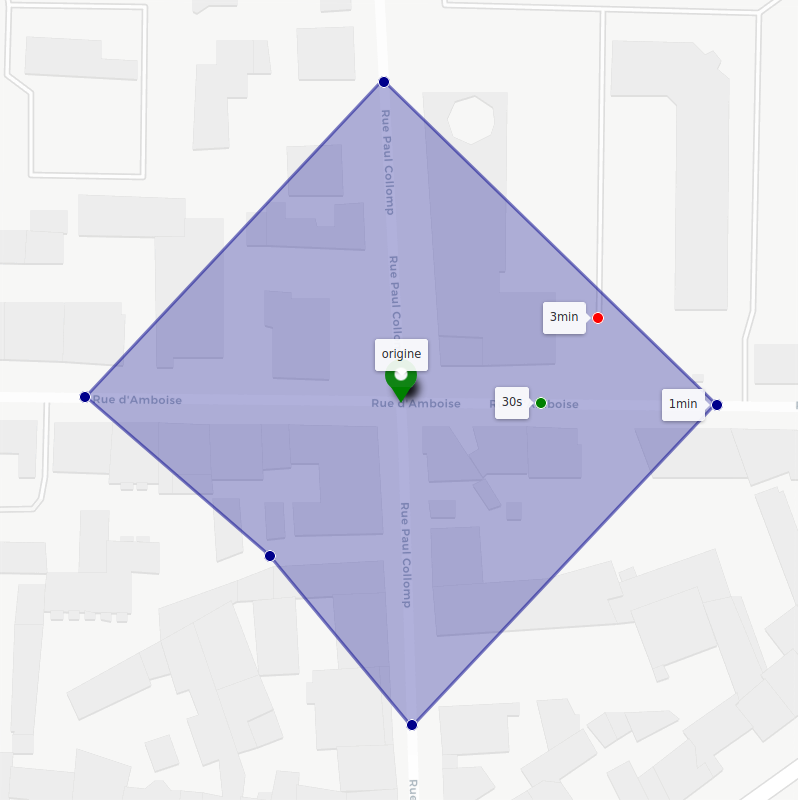
Selon les algorithmes utilisés pour calculer les points accessibles et cette approximation, la représentation d’une même isochrone peut varier drastiquement :

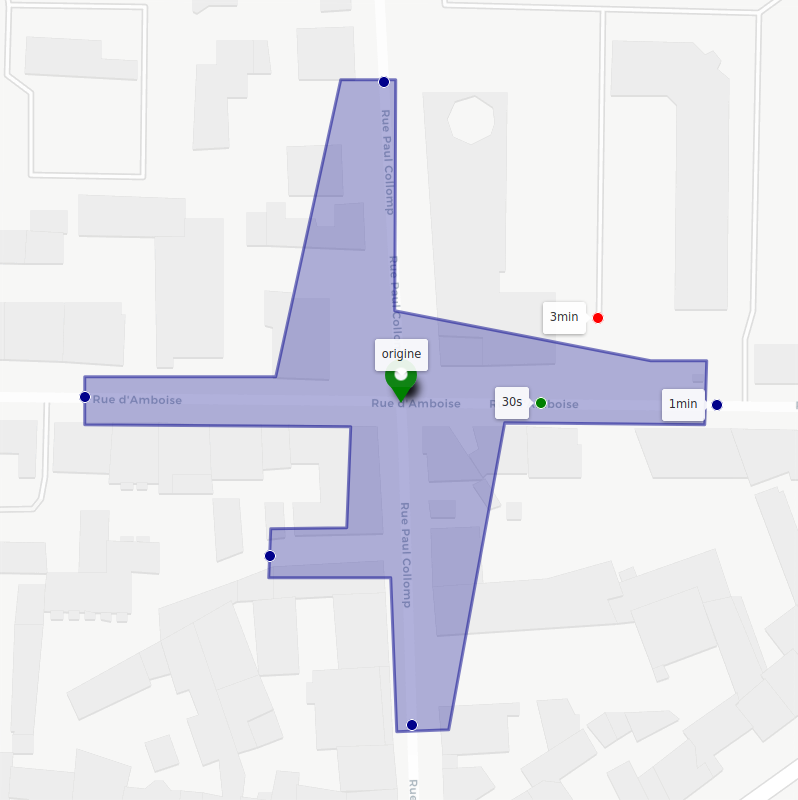
Les limites de la représentation des isochrones

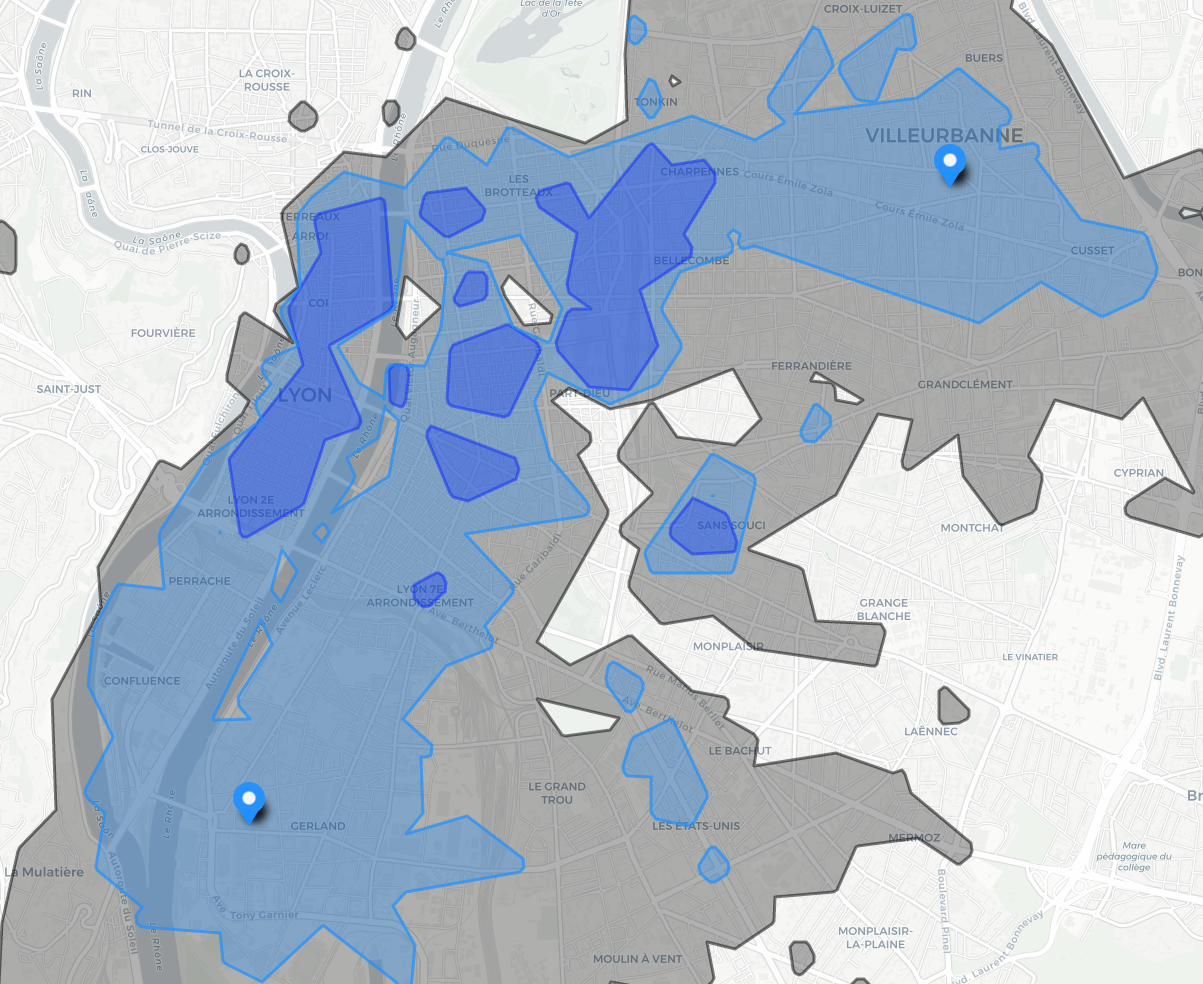
On a vu avec les exemples précédents que la représentation des isochrones dépend beaucoup de la précision avec laquelle elle est approximée. On gardera donc à l’esprit le fait qu’une zone peut apparaître accessible alors qu’elle ne l’est pas et vice-versa. La présentation manichéenne sous forme de zone bien bornée peut donner une impression d’exactitude, alors qu’il faut se figurer la frontière d’une isochrone comme une zone de flou. On peut préférer à ce titre une superposition de plusieurs isochrones pour représenter cette imprécision à la frontière. Par exemple pour un cas d’utilisation concret on peut préférer les isochrones à +/- 10 % du temps cible, ici les isochrones à 27 minutes (bleu sombre) et 33 minutes (bleu clair) permettent d’évaluer l’étendue potentielle de l’erreur commise en regardant uniquement l’isochrone à 30 min (le liseré blanc):

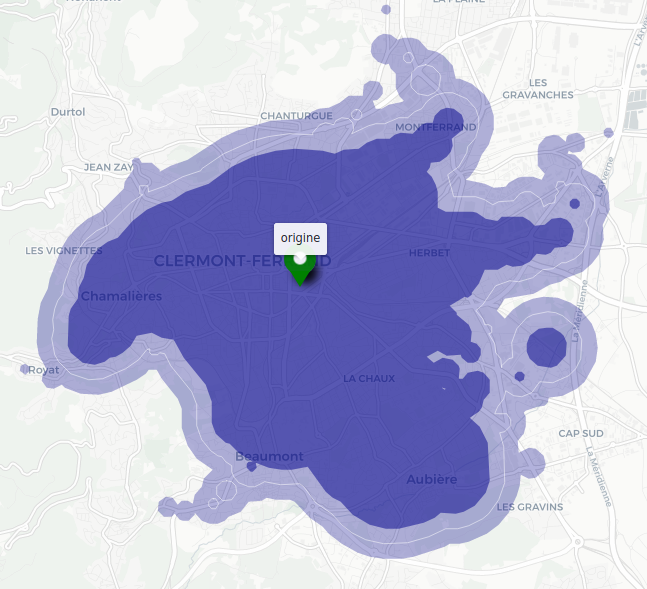
Extension de l’isochrone à plusieurs origines

Puisqu’une isochrone n’est qu’un ensemble de points de l’espace, on peut vouloir étendre son concept à plusieurs origines ou destinations, et la façon immédiate et naturelle est de procéder avec les opérations ensemblistes classiques. Citons par exemple :

Intersection d’isochrones

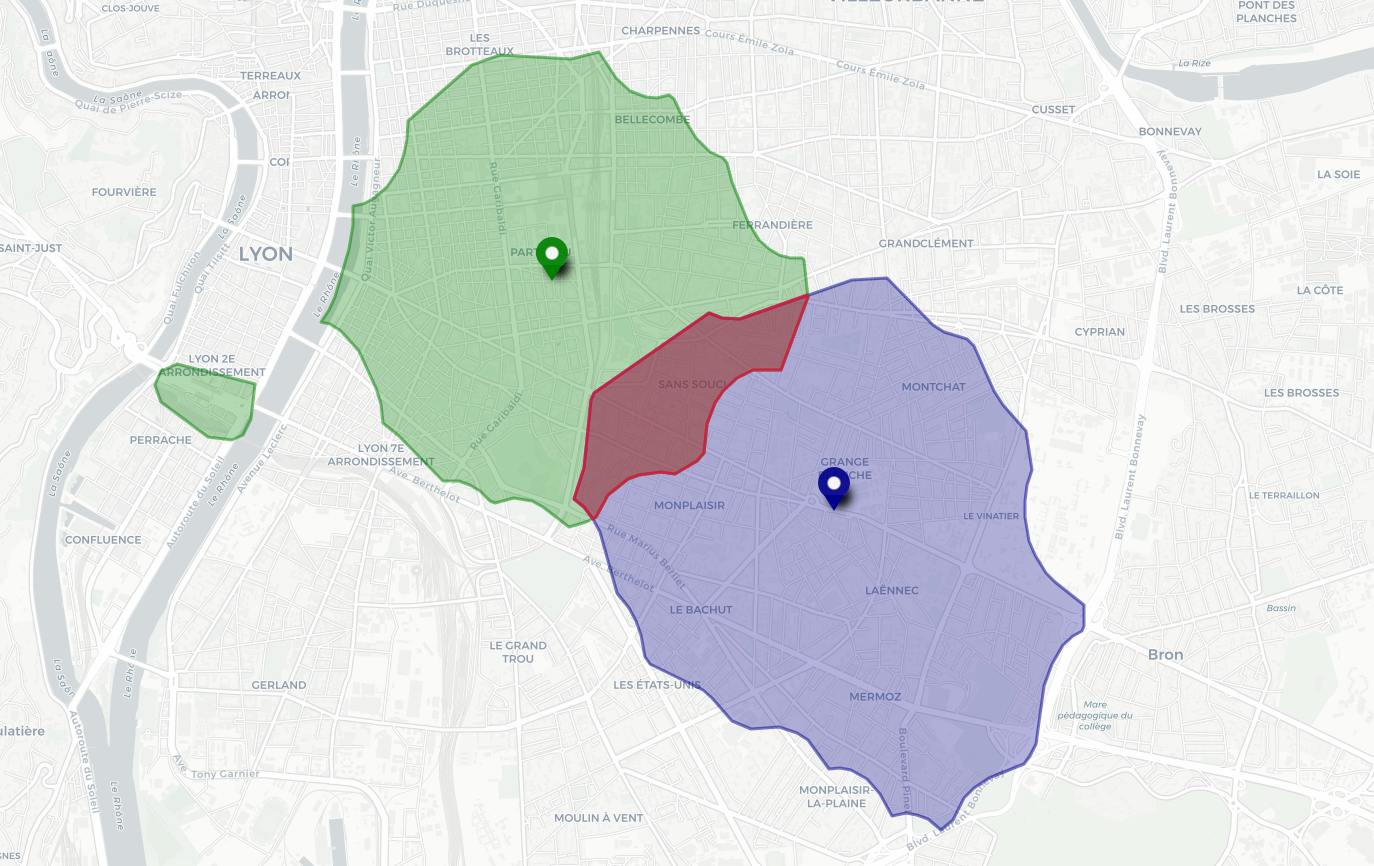
L’intersection de plusieurs isochrones permet de découvrir la zone dans laquelle le temps d’accès est borné pour chacun des points d’origine. C’est-à-dire qu’elle montre des propriétés du type « tout le monde met au maximum x minutes ». On peut ainsi obtenir des zones préférentielles de rendez-vous pour plusieurs personnes. Bien sûr une telle intersection peut être vide, c’est-à-dire qu’il peut n’exister aucun endroit satisfaisant à la condition de temps d’accès maximal. C’est une représentation utilisable pour déterminer une zone optimale d’implantation, bien qu’il puisse être plus intéressant de procéder à d’autres optimisations (cf ci-après, les mésochrones).

Union d’isochrones

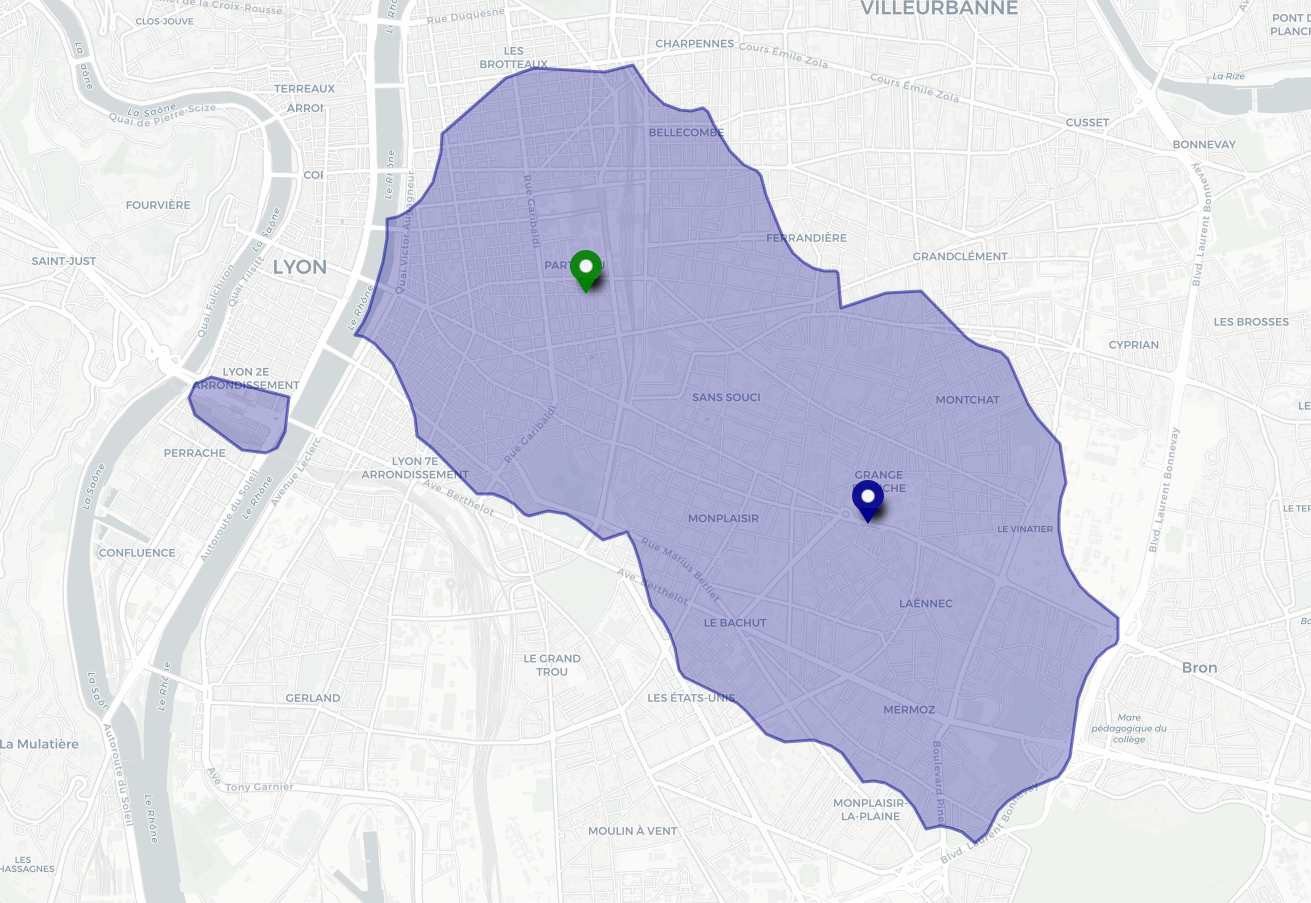
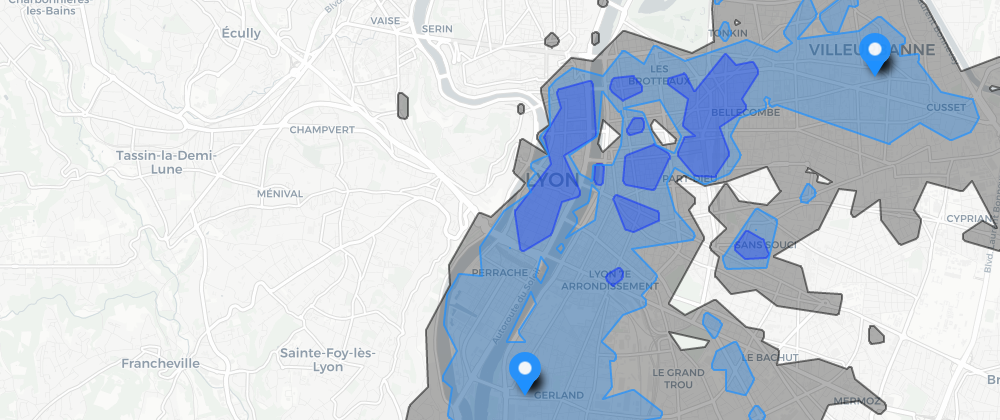
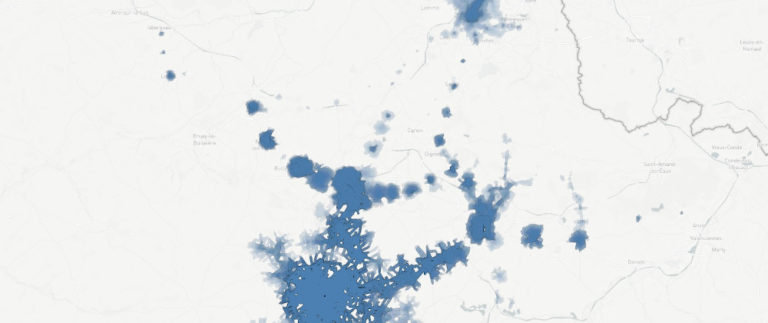
En faisant l’union de plusieurs isochrones on obtient la zone de l’espace accessible en un temps t depuis au moins une des origines des isochrones. C’est la représentation que Modelity utilise dans ses études pour les entreprises implantées sur plusieurs sites. En effet l’union des isochrones construites à partir de chaque site donne la zone dans laquelle le temps d’accès à au moins un site est borné. Ça peut donc être le bassin d’emplois auquel cette entreprise a accès, ou bien sa zone de chalandise.

Les mésochrones

On a vu comment utiliser des opérations ensemblistes sur les isochrones pour représenter des données temporelles concernant plusieurs origines à la fois. Dans les deux cas présentés nous obtenons des propriétés très exclusives. Pour l’intersection d’isochrones on a une contrainte très forte : tout le monde met un temps t au maximum. Pour l’union d’isochrones on a une contrainte très faible : au moins une origine met un temps t au maximum. Avec les mésochrones nous allons exprimer une contrainte plus nuancée, à savoir que tout le monde met en moyenne un temps t.

Définition formelle

Nous proposons donc la définition de mésochrones, ou zones de temps d’accès moyen borné, par extension du concept de base des isochrones en considérant a priori plusieurs origines. Ces mésochrones représentent par exemple les zones pour lesquelles les temps d’accès moyens pour plusieurs personnes sont minimaux. Il s’agit donc de zones de rendez-vous privilégiées, ou de zones dans lesquelles l’implantation d’un site pour une entreprise aboutirait à un temps d’accès moyen minimal pour ses salariés.

Formellement, on appelle une mésochrone M_Ω,t d’origines Ω et de temps t l’ensemble des positions P qui sont accessibles en un temps moyen inférieur à t pour chaque origine O de Ω³. Soit, en notant d(O,P) la méthode d’obtention du temps de trajet minimal d’un point O à un point P :

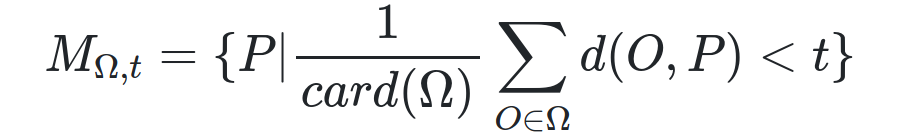
Comme le temps d’accès moyen minimal depuis plusieurs origines est en général non nul (sauf si toutes ces origines sont confondues) on utilisera en fait une définition décalée par ce temps d’accès moyen minimal t_min. Aussi la mésochrone M_Ω,Δt d’origines Ω et de temps Δt devient :

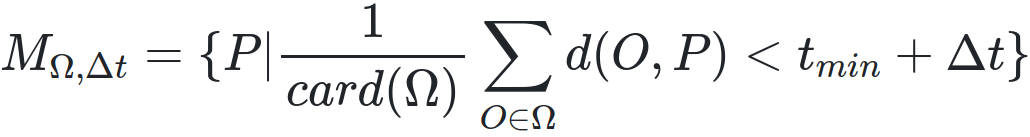
Nous avions précédemment défini les unions et intersections d’isochrones à partir d’opérations ensemblistes sur les isochrones de chaque origine, mais nous pouvons remarquer qu’elles se définissent aussi de façon très similaire aux mésochrones. À savoir :

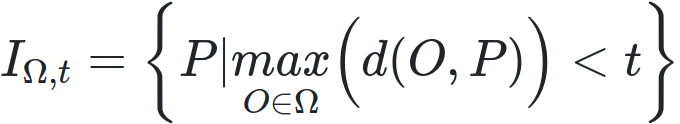
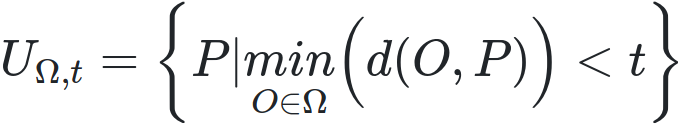
en notant I_Ω,t et U_Ω,t respectivement l’intersection et l’union des isochrones d’origines dans Ω et de temps t. La similitude dans ces trois expressions vient du fait qu’il s’agit bien, pour l’union et l’intersection d’isochrones ou la mésochrone, de borner une zone de l’espace par rapport à un calcul fait sur les temps d’accès depuis plusieurs origines. Il vient d’ailleurs trivialement⁴ que :

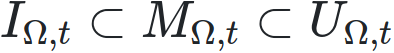
C’est-à-dire que pour un temps t donné, l’intersection des isochrones depuis plusieurs origines est incluse dans la mésochrone de ces origines, elle même incluse dans l’union de ces isochrones, comme illustré dans la représentation suivante :

Exemples d’utilisation

Nous utilisons ces définitions dans les exemples suivants, où nous allons comparer les intersections d’isochrones et les mésochrones pour différentes configurations de points d’origines. Les temps d’accès sont calculés à partir des points indiqués sur les cartes, et se limitent aux trajets à pied et en transport en commun.

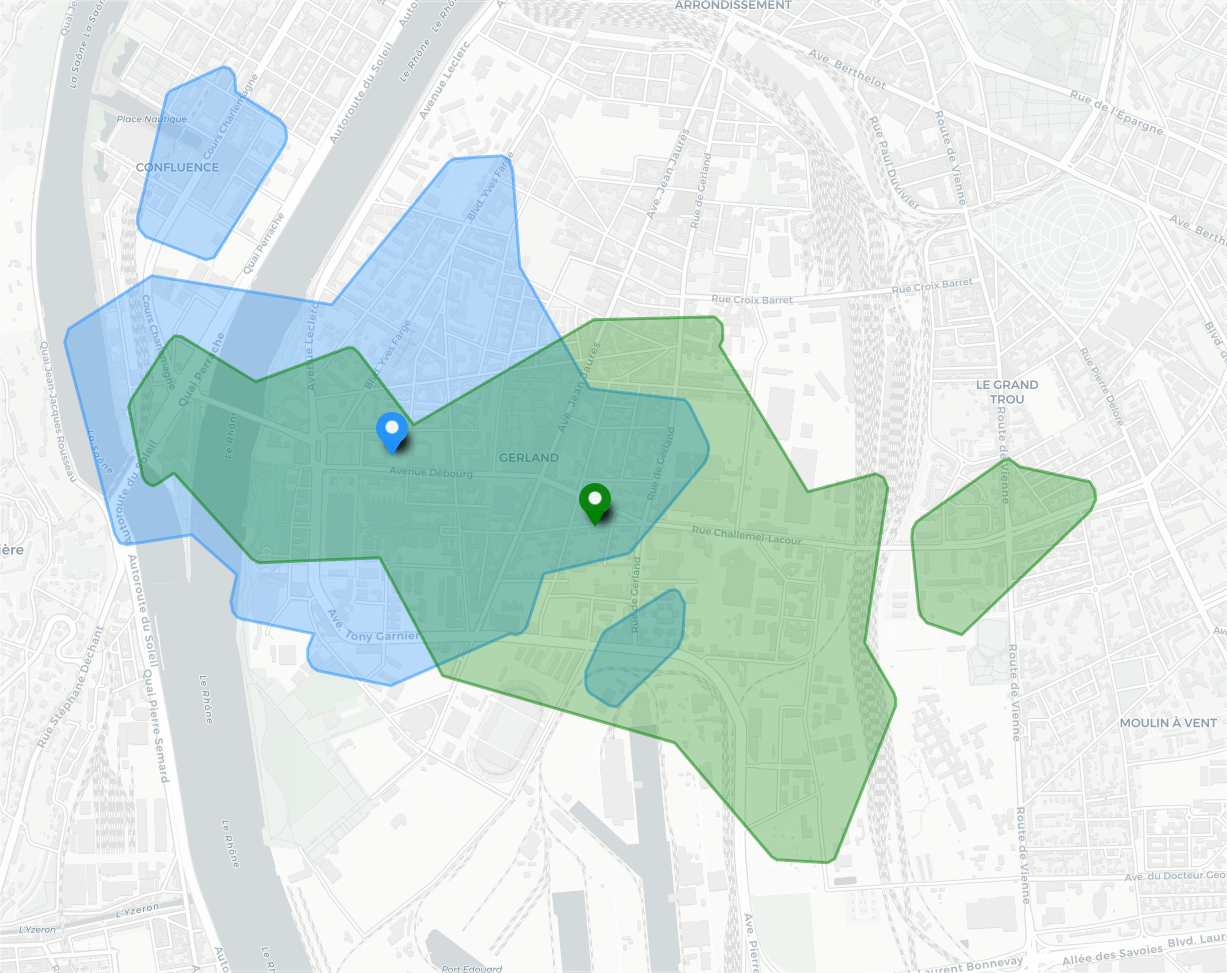
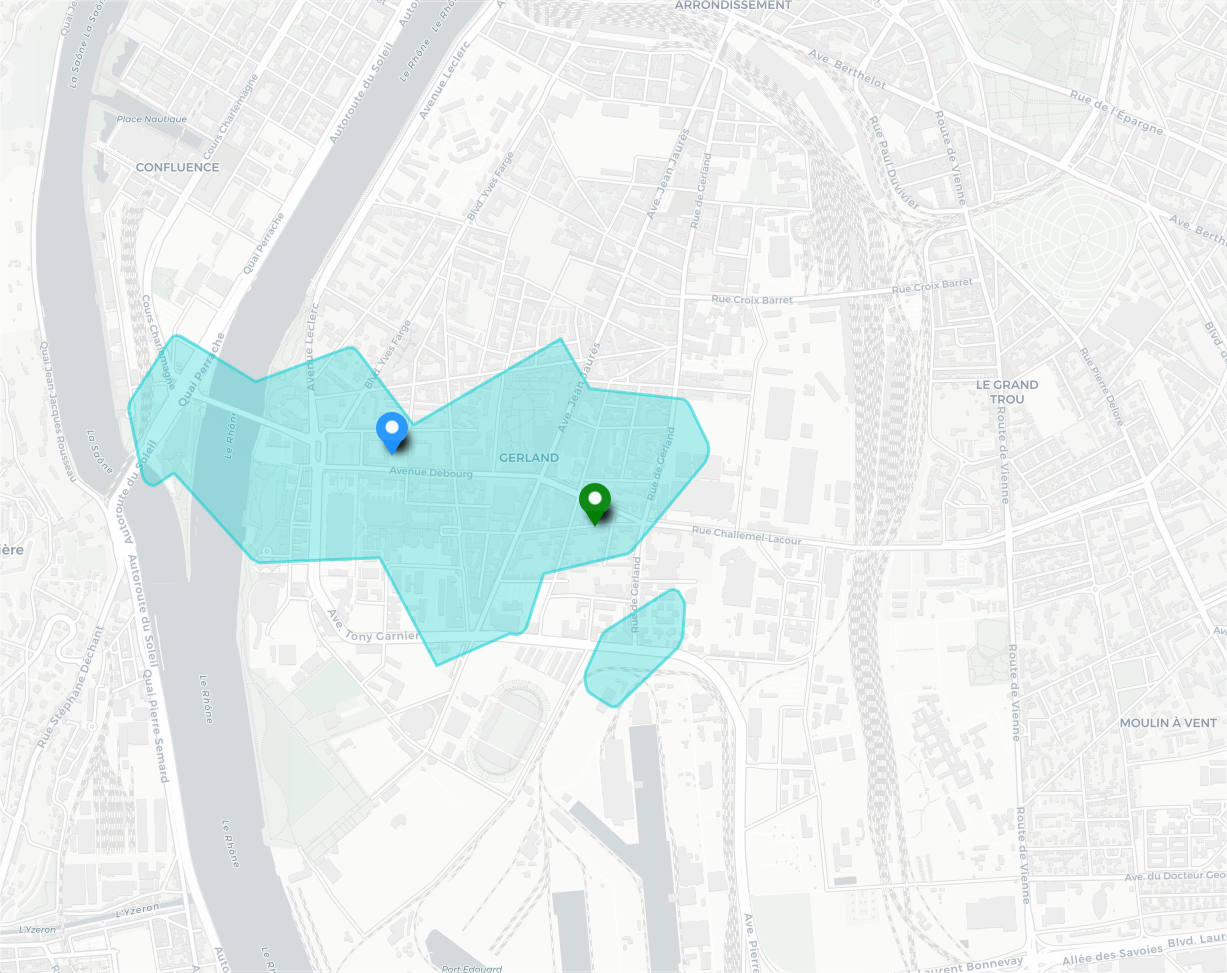
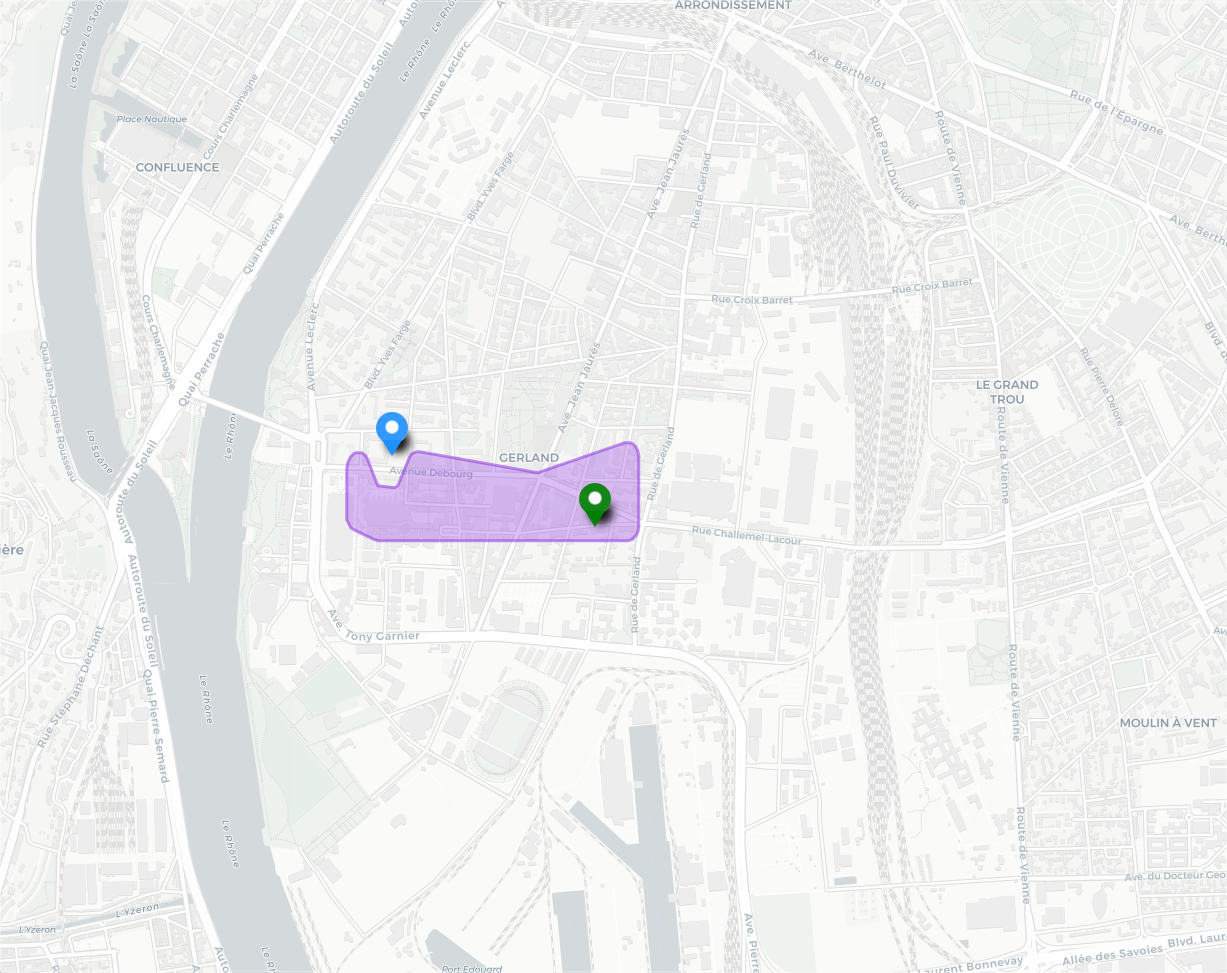
Dans cet exemple l’intersection d’isochrones et la mésochrone sont assez similaires. Le temps d’accès minimal moyen étant de 4 minutes, la mésochrone, dont le Δt vaut 5 minutes, englobe donc une zone de temps d’accès moyen borné à 9 minutes. À l’intérieur de l’intersection des isochrones le temps d’accès est borné à 15 minutes pour chaque origine.

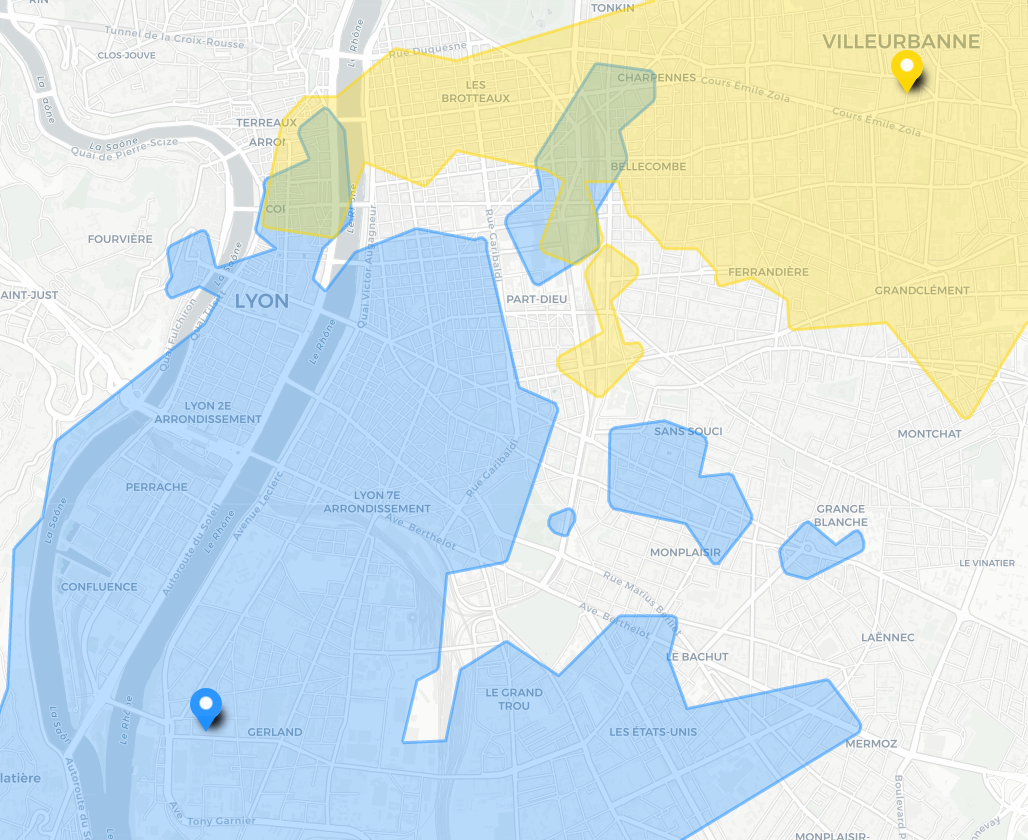
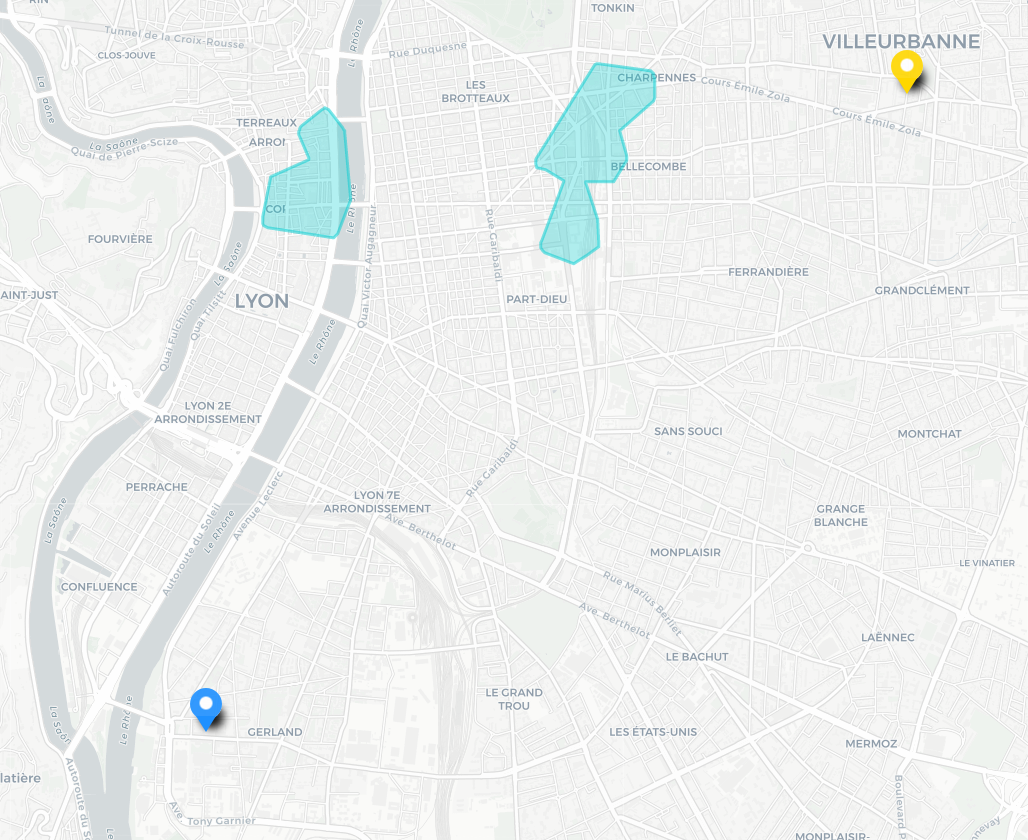
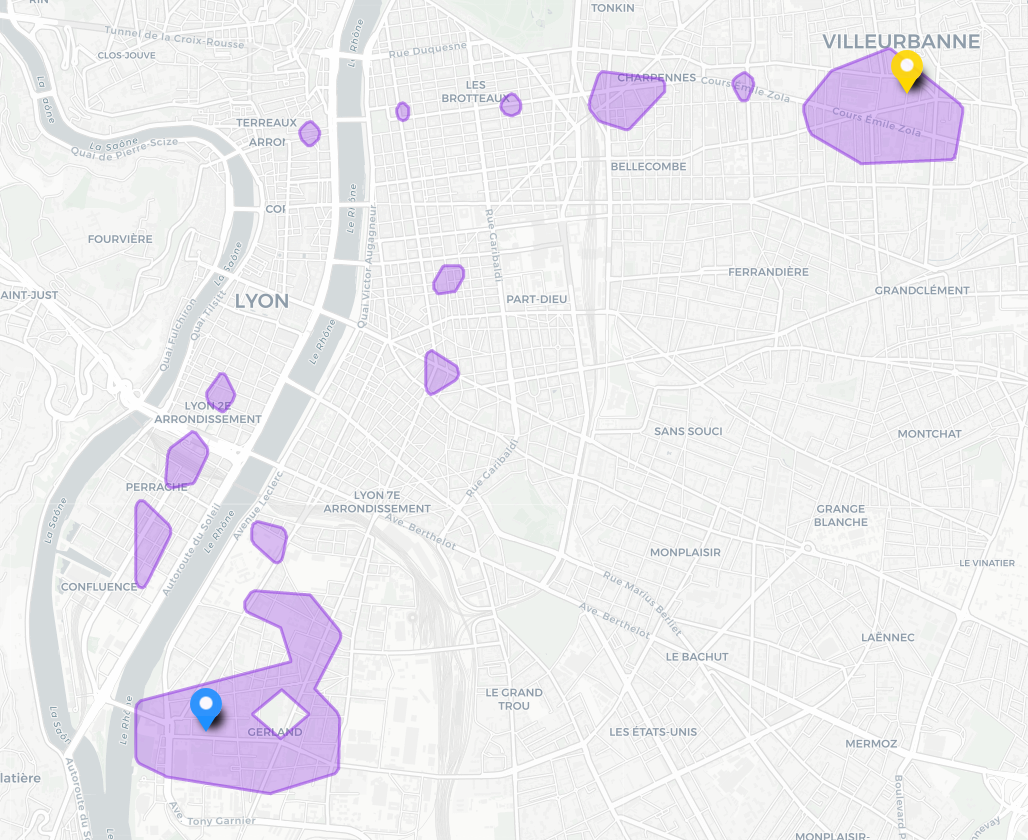
Pour des origines éloignées la différence est plus marquée. On peut noter en particulier que la mésochrone fait apparaître des zones autour de chaque origine. En effet dans ces zones une des origines est favorisée au maximum alors que l’autre est défavorisée. Lors du calcul de la moyenne des temps d’accès il peut se produire que cette option soit favorable, comme dans le cas présent. En revanche pour l’intersection des isochrones chaque origine est garantie d’avoir un temps d’accès borné (ici à 30 minutes) ce qui interdit qu’une seule des origines soit très défavorisée. Pour information, le temps d’accès minimal moyen dans cet exemple est de 19 minutes, la mésochrone englobe donc une zone dont le temps moyen d’accès est inférieur à 24 minutes.

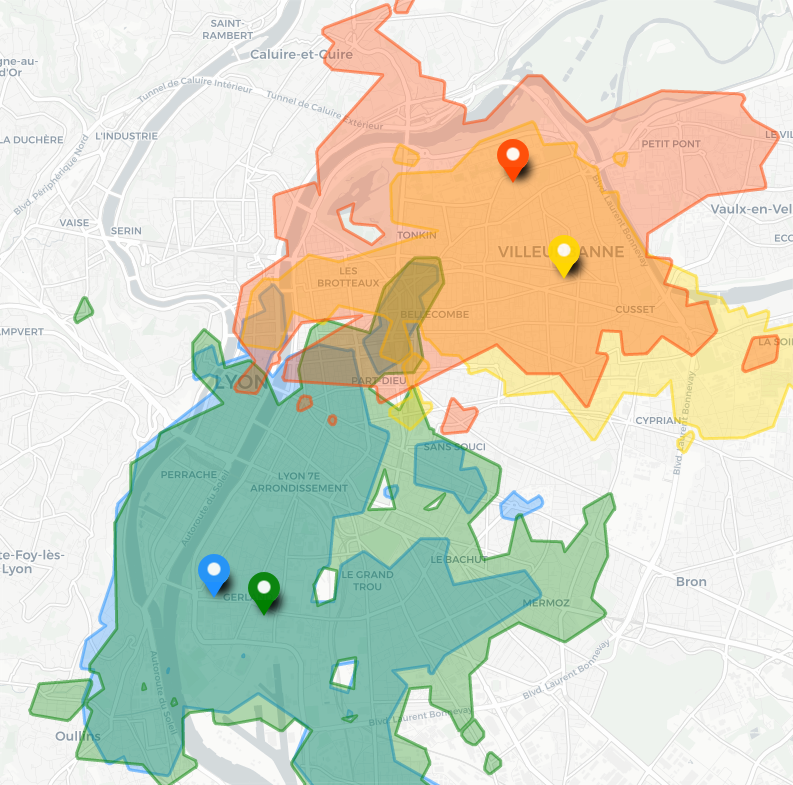
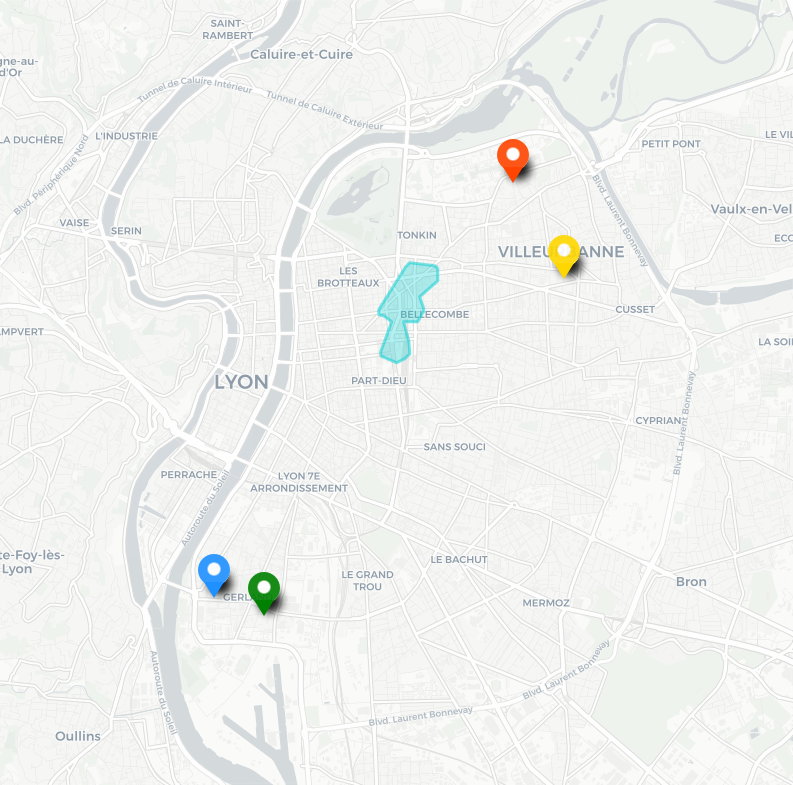
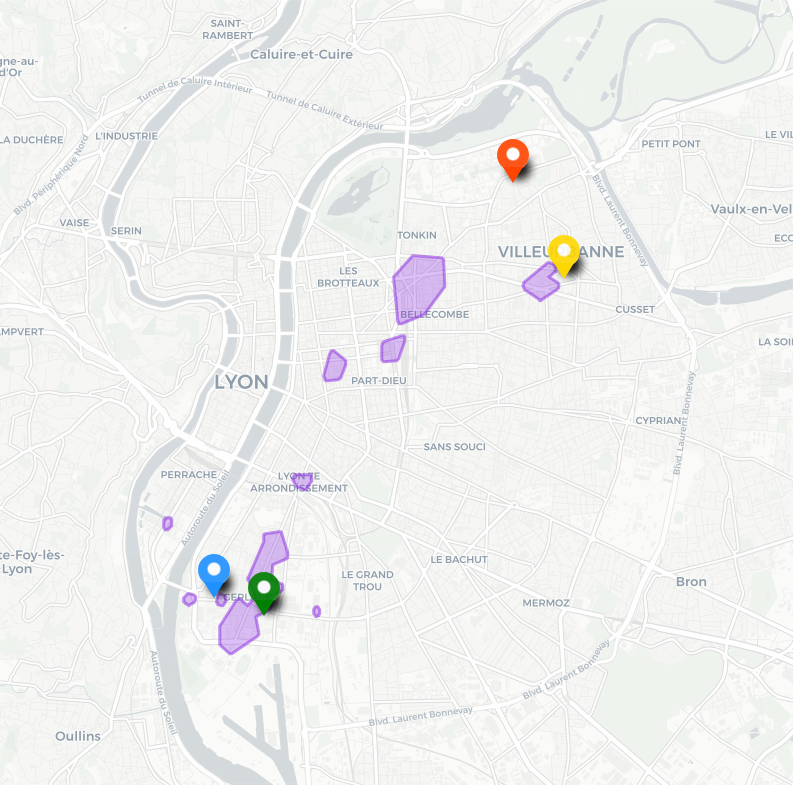
Dans cet exemple le temps d’accès minimal moyen est également de 19 minutes, la mésochrone englobe donc aussi une zone dont le temps moyen d’accès est inférieur à 24 minutes. Lorsque la situation se complexifie il peut devenir difficile d’obtenir une intersection d’isochrones non vide. Ici la zone est assez réduite par rapport aux cas précédents. En pratique, dès qu’un seul point suffisamment éloigné est ajouté au problème il n’est plus possible de garantir un temps d’accès maximal raisonnable pour chaque origine. Les mésochrones offrent une approche plus globale au problème de la représentation des zones optimales en temps d’accès, en apportant leur propre problème de mettre potentiellement de côté les cas limites.

Enfin il est bien sûr toujours possible de composer ces différentes zones pour affiner les propriétés temporelles qu’elles dévoilent. Par exemple, implanter son entreprise dans un quartier minimisant les temps de trajet de tous les salariés et en garantissant que le responsable de site puisse accéder aux bureaux en moins de 15 minutes.

Les propriétés dont les isochrones et les mésochrones rendent compte sont donc complémentaires, et quand elles sont utilisées à bon escient elles permettent de répondre de façon très graphique à des problèmes d’optimisation temporelle. Il faut dans tous les cas garder à l’esprit les approximations effectuées lors de leur calcul et bien les considérer comme des outils graphiques et indicatifs plutôt que comme le reflet de vérités absolues sur un territoire.

---

1. ↥ Au sens strict la courbe isochrone est en fait l’ensemble des points exactement accessible en un temps t, c’est-à-dire une partie de la frontière de cet ensemble.
2. ↥ On peut définir de façon symétrique les isochrones vers une destination D comme l’ensemble des points pour lesquels D est accessible en un temps inférieur à t.
3. ↥ Et symétriquement pour un ensemble de destinations au lieu d’origines.
4. ↥ Preuve : tous les points dans l’intersection des isochrones ont un temps d’accès inférieur à t depuis chaque origine, la moyenne de leur temps d’accès sur toutes les origines est donc inférieure à t (I_Ω,t ⊂ M_Ω,t); tous les points en dehors de l’union des isochrones ont un temps d’accès supérieur à t depuis chaque origine, la moyenne de leur temps d’accès sur toutes les origines est donc supérieure à t (^CU_Ω,t ⊂ ^CM_Ω,t)

Cartes utilisées dans cette page: Map tiles by CartoDB, under CC BY 3.0. Data by OpenStreetMap, under ODbL.